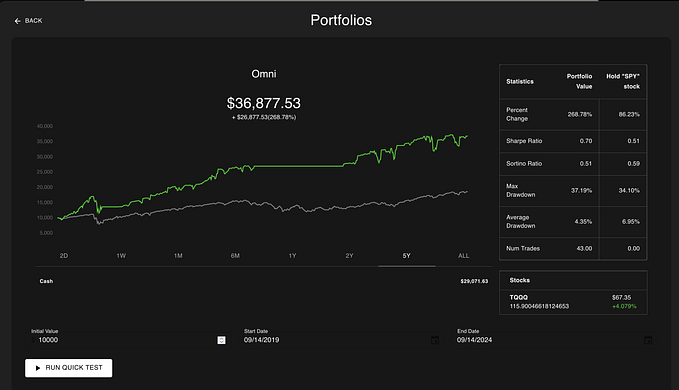
Fearless Trigonometry — The Pythagorean Identities
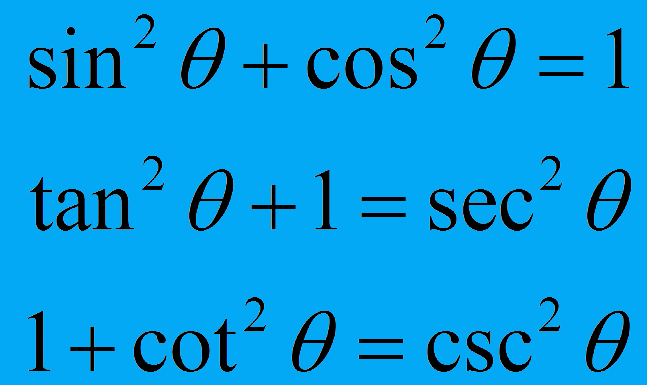
Mathematicians have labored for ages to get relationships within triangles along side other polygons. one among the famous and beneficial relationships ended up being uncovered by the Greek mathematician called Pythagorus. He found the edges of a right-angled triangle are related within the following way:
When the lengths of every of the shorter two sides (the legs) of the proper triangle are squared and therefore the squares added together, the entire is that the same because the length of the 3rd side (called the hypotenuse) squared. So do you have to notice a right-angled triangle , confine mind that the lengths of the two smaller sides are associated with the length of the longest side.
If a private had time to make three external squares from all sides of any right-angled triangle , you’ll discover the smaller squares end in a stimulating relationship as compared to the large square.
A triangle whose edges measure 3 units, 4 units, then five units is one among the foremost well-known triangles in only about all of mathematics. Squaring each of the two smaller sides yields nine sixteen Equals 25 sq units. The longer side is five units, which suggests its square has a neighborhood of twenty-five square units. This arrangement holds true for every and each right-angled triangle .
Many problems that affect right triangles yield decimal answers. However, there are many samples of whole numbers combinations that are possible in right triangles. a number of these are:
three, four, five
six, eight, ten
five, twelve, thirteen
seven, twenty-four, twenty-five
eight, fifteen, seventeen
Each of the above combinations represent the three lengths of a right-angled triangle . In class, teachers often begin to show the concept of the Pythagorean Theorem using integer examples. Later in school , many of the answers may contain one or more sides whose lengths aren’t whole numbers.
In a right-angled triangle , the two smaller sides are legs and therefore the longest side is understood as a hypotenuse. Usually a stands out because the shorter of the 2 legs and b is typically the longer of the legs. In some cases, a is that the identical length as b. alright triangles contain a lengthiest side that’s directly across from the proper angle. This longest side is represented by the variable “c” and it’s mentioned because the hypotenuse.
The Pythagorean Theorem is most remembered by the equation a² + b² = c². to increase this to trigonometry, we let (x, y) be an ordered pair on the unit circle, that’s the circle centered at the origin and having radius adequate to 1. By our famous theorem, we’ve that x² + y² = 1, since the x and y coordinates carve out a right-angled triangle of hypotenuse 1. it’s from this construct that we obtain the trigonometric identities, which we explore here.
Let us recall the definitions of the sine and cosine functions on the unit circle of equation x² + y² = 1. so as to know this, it’s important to understand that the x-coordinate is that the abscissa and therefore the y-coordinate is that the ordinate. With this in mind, we define the sine because the ordinate/radius and therefore the cosine because the abscissa/radius. Denoting x and y because the abscissa and ordinate, respectively, and r because the radius, and A because the angle generated, we’ve sin(A) = y/r and cos(A) = x/r.
Since r = 1, sin(A) = y and cos(A) = x within the previous definitions. Since we all know that x² + y² = 1, we’ve sin²(A) + cos²(A) = 1. this is often our first Pythagorean identity supported the unit circle. Now there are two others supported the opposite trigonometric functions, namely the tangent, cotangent, secant, and cosecant. Fortunately though we’d like only memorize the primary one because the opposite two come free, as i used to be taught by my Calculus I professor during my freshman year in college. The thanks to derive the opposite two identities is predicated on the connection between tangent (tan) and cotangent (cot); and secant (sec) and cosecant (csc).
Reciprocal Identities
To derive the opposite two Pythagorean identities, we use the reciprocal identities below:
csc(A) = 1/sin(A)
sec(A) = 1/cos(A)
cot(A) = 1/tan(A)
tan(A) = sin(A)/cos(A)
As my college calculus professor demonstrated to me, we start with the primary one and successively derive the others as follows:
(1) sin²(A) + cos²(A) = 1
To get the Pythagorean identity involving tan and cot, we divide the whole equation by cos²(A). this provides
sin²(A)/cos²(A) + cos²(A)/cos²(A) = 1/cos²(A)
Using the reciprocal identities above, we see that this equation is that the same as
tan²(A) + 1 = sec²(A)
To get the Pythagorean identity involving cot and csc, we divide equation (1) above by sin²(A), again resorting to our reciprocal identities to get
sin²(A)/sin²(A) + cos²(A)/sin²(A) = 1/sin²(A)
Upon simplifying, this provides our third Pythagorean identity:
1 + cot²(A) = csc²(A)
That’s really all there’s thereto . which my dear friends is how we use one identity to get two others for free of charge . Maybe there are not any free lunches in life, but a minimum of sometimes there are free lunches in mathematics. Thank God!
Joe may be a prolific writer of self-help and academic material and is that the creator and author of over a dozen books and ebooks which are read throughout the planet . he’s a former teacher of high school and college mathematics and has recently returned as a professor of mathematics at an area junior college in New Jersey.
This is the fourth during a series of short articles explaining the utilization of ancient musical modes to assist mental soundness and inner harmony. the primary article was an summary of the subject; the second addressed the Phlegmatic Temperament; and therefore the third, with the Choleric. this text will affect balancing the Sanguine Temperament especially .
I will also go a touch into the traditional Greek astrological conception of the Four Temperaments and therefore the Eight Pythagorean modes.
Sanguine personalities are typically the “life and soul of the party”. When in balance, the sanguine temperament gives the subsequent qualities:-
* Good Cheer
* Sociable nature
* Warm personality
* Enthusiastic nature
* Optimism
* Friendliness
* good humor
When the Sanguine temperament is out-of-balance it produces:-
* Lack of Follow-through
* Punctuality issues
* Forgetfulness
* Wears Heart on his/her sleeve. (Too naive and trusting)
* Flighty
Listening to the Lydian mode increases the great qualities of the Sanguine. So, if we might wish to be more sociable, optimistic, etc. we should always hear that mode. If, however, we are affected by an excessive amount of of these qualities, (perhaps we’ve been overdoing the social life a touch , or need grounding), we could hear the hypolydian mode.
The Temperaments and Astrology
The phlegmatic is increased by the facility of the SUN and decreased by the MOON;
And the melancholic is increased by SATURN. there’s no second planet related to the melancholic, but we’ll affect this during a moment.
The Modes and therefore the Planets
There are eight modes but only seven recognized planets in astrology. this is often the rationale why the melancholic humour has just one planet related to it.
The dorian mode is ruled by the SUN. So, among other things, it’s good for aiding wakefulness and application . The hypodorian, on the opposite hand, is ruled by the MOON. So it’s good for helping us to nod off .
The phrygian mode is ruled by MARS. The hypophrygian, on the opposite hand, is ruled by MERCURY. As Mercury may be a messenger, this mode is beneficial for decreasing the autonomous nature of the Choleric, and replacing it with a willingness to speak on equal terms with others.
a
The Lydian mode is ruled by JUPITER. Jupiter is that the “bringer of jollity”, hence the importance of this mode for increasing sanguine tendencies. The hypolydian, however, is ruled by VENUS. Venus is that the Goddess of affection . As such, she cares with much deeper emotions (perhaps we could even say “sadder” emotions) than the frothy experience of the Sanguine. therefore the hypolydian is sweet for grounding the sanguine in us.
The Construction of the Modal Scales
The eight Pythagorean modes are often quickly obtained by starting with a standard major diatonic scale . allow us to take the size of C major for simplicity, because it is formed up solely of white notes on the fingerboard .
The scale of C major runs like this:
C D E F G A B C
The dorian mode is that the same scale, starting on the second note (D). For therapeutic purposes, the mode only features a range of seven notes, so it runs:
D E F G A B C
The lydian starts on F;
And the mixolydian begins on G.
These are the four “authentic modes”. The four “plagal modes” are the hypodorian, hypophrygian, hypolydian and hypomixolydian. These balance their authentic companions, and are to be found starting a 4th below. So, as an example , the hypodorian starts a 4th below the dorian, on the note ‘A’.
For therapeutic purposes, (assuming we are using C because the root major), melodies should start on A (the “dynamic middle”) and finish on rock bottom note of the mode (the “Final”). The note ‘A’ is defined as being the 6th note within the root major diatonic scale , which, during this example is C major. This note (the 6th of the basis major) corresponds to the SUN. By starting on A, and returning thereto often, then finishing on the ultimate , the facility of the Sun is drawn right down to the earth that rules the mode. So, within the case of the Lydian, the solar energy (note ‘A’) is drawn right down to Jupiter (F, the ultimate of the mode, or the 4th of the basis major).
If you’re on the ball, you’ll have noticed that the dorian and therefore the hypomixolydian are identical, as they both begin on D. But the hypomixolydian may be a special mode with a rather different rule. Melodies should start on A, like the opposite modes, but they ought to finish, not on D, but on the ultimate of the authentic mode (the Mixolydian), which is G.
The hypomixolydian mode isn’t linked to a planet intrinsically , but is taken into account to be the mode of universal, cosmic bliss. it’s therefore good for all therapeutic purposes, and is related to the entire Cosmos, (or the “fixed stars” as they were known in past . this is often the mode that’s wont to counteract the facility of SATURN.
The next article will affect the last of the Temperaments: the Melancholic. we’ll also go a touch more deeply into composing or improvising modal melodies.
Cepheus may be a composer, pianist and teacher with an interest within the development of consciousness. He has studied widely within the field of self development, particularly within the application of sound or music to worry related problems.